Quote:
Originally Posted by Jobbo
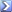
I came up with my own higher precision version in 40bytes. Not sure if anyone can spot some extra size optimizations, it's late here!
|
I was experimenting with Bhaskara's algorithm today, and with a 64-bit div it could *almost* be done in 32 bytes (it still overflows at +/-pi). It works with rather large numbers (when you include 16384 amplitude and 1024 table size)

.
Divisor includes 5*pi^2, and with pi being 512 this is then 327680. Swap does no good (kills precision), numbers have to be further divided by >5, so 8. And then I remembered your code, 40960 and those crazy shifts.
So I've integrated 2 optimizations into your code and it's 38 bytes now:
- first opt is what I said in my previous post (replace multiplication with a1 increments), which then enables
- second opt is that you can replace 40960-a*b with a counter that starts at 40960 (actually 327680=5*65536 pre-shift) and then decrease it by the same amount you increase a*b (which is a1)
Code:
moveq #0,d0
moveq #5,d1
swap d1
move.w #511+2,a1
.loop move.l d0,d3
move.l d1,d2
lsl.l #8,d3
lsl.l #8-3,d3
lsr.l #3,d2
divu.w d2,d3
move.w d3,(a0)+
neg.w d3
move.w d3,(1022,a0)
subq.l #2,a1
sub.l a1,d1
add.l a1,d0
bne.b .loop